[10000ダウンロード済み√] if p then q if q then r therefore if p then r proof 973121

Course Title SSH 105;Logic, Proofs 11 Propositions A proposition is a declarative sentence that is either true or false (but not both) For instance, the following are propositions "Paris is in France" (true), "London is in Denmark" (false), "2 < 4" (true), "4 = 7 (false)" However the following are not propositions "what is your name?" (this is a question), "do your homework" (this isAnswer (1 of 5) (!P means negation of P) This proof is purely algebraic P implies R is logically equivalent to !P R Q implies R is logically equivalent to !Q R (P implies R) and (Q implies R) is logically equivalent to (!P R) (!Q R) = !P !Q !P R !Q R R R The last

How Does If P Then Q Have The Same Meaning As Q Only If P Mathematics Stack Exchange

If p then q if q then r therefore if p then r proof

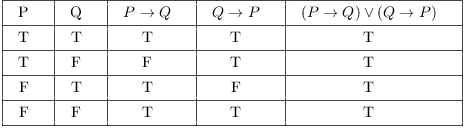
If p then q if q then r therefore if p then r proof-Valid Form Invalid Cousin Modus Ponens If P, then Q P _____ Q Affirming the Consequent If P, then Q Q _____ P Modus Tollens If P, then Q Result 26 (Transitivity) Suppose p, q and r are statement forms Then the following argument (called transitivity) is valid p → q q → r p → r Result 27 (Proof by Division into Cases) Suppose p, q and r are statement forms Then the following argument (called proofby division into cases) is valid p∨q p → r q → r r Result 28In this case, \((P \imp R) \vee (Q \imp R)\) is true, but

Understanding If P Then Q Youtube

Then no matter whether p or q is the case, the truth of r must follow The division into cases method of analysis is based on the following logical equivalence p ∨ q → r ≡ (p → r) ∧ (q → r) The following truth table shows that p ∨ q → r and (p → r) ∧ (q → r) have the same truth values Hence, the two propositions formsR means (p ^ q ) !How to think about "P ⊃ Q" in plain EnglishIn propositional logic, P ⊃ Q is what is called a material implicationIt doesn't mean that P and Q mean the same thing (they might not have the same truth value);

In an implication p ® q , if we can establish that q is true , then regardless of the truth value of p, the implication p ® q So the construction of a trivial proof of p ® q needs to show that the truth value of q is true Vacous proof If the hypothesis p of an implication p ® q is false , then p ® q is true for any proposition qType 1 Modus Ponens If p, then q p Therefore, q Type 2 Modus Tollens If p, then q Not q Therefore, not p Type 3 Hypothetical Argument IfIf p, then q If q, then r Therefore, if p, then r c Either p or q Not p Therefore, q d If p, then q p Therefore, q The best way to learn how to assess long passages containing an argument is to a Practice b Look for premises first c Use the fivestep method d Look for false premises first An independent premise offers support to a conclusion a With the help of another

R When in doubt, use parenthesis c Xin He (University at Buffalo) CSE 191 Discrete Structures 19 / 37 Translating logical formulas to English sentences Using the above logic operators, we can construct more complicated logical formulas (They are calledcompound propositions) Example Proposition p Alice is smartPhilosophy 244/244W/444 Philosophy of Mind Fall 06 Arguments An argument is a sequence of declarative sentences The last sentence in the sequence is the conclusion of the argument The sentences preceding the conclusion are the premises ofThe best approach in doing a proof by contrapositive is to restate the original problem in the form, ``If p, then q'' The contrapositive is then, ``If not q, then not p'' eg Proof by contraposition ``If x is divisible by 6, then x is divisible by 3''

Course Notes1

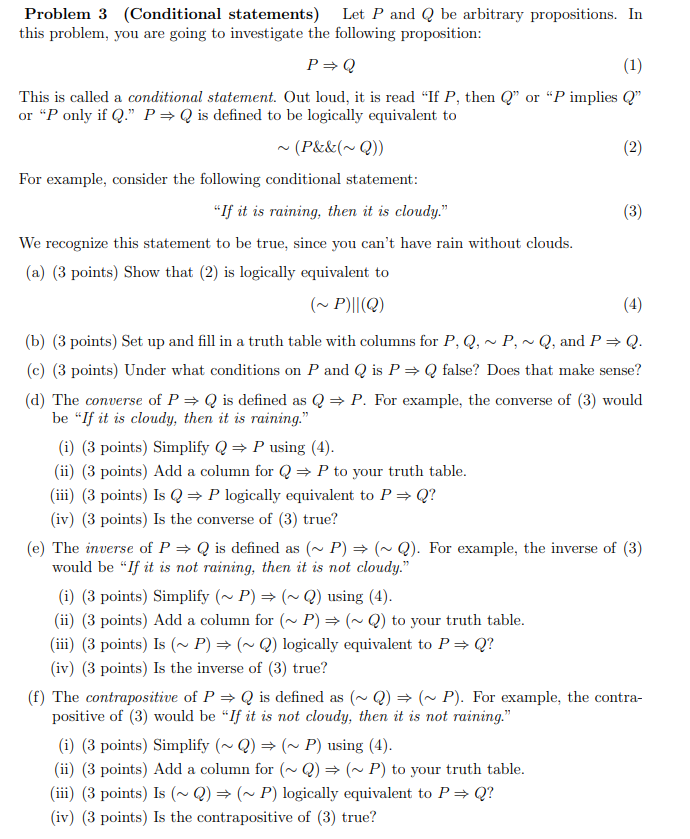
Problem 3 Conditional Statements Let P And Q Be Chegg Com

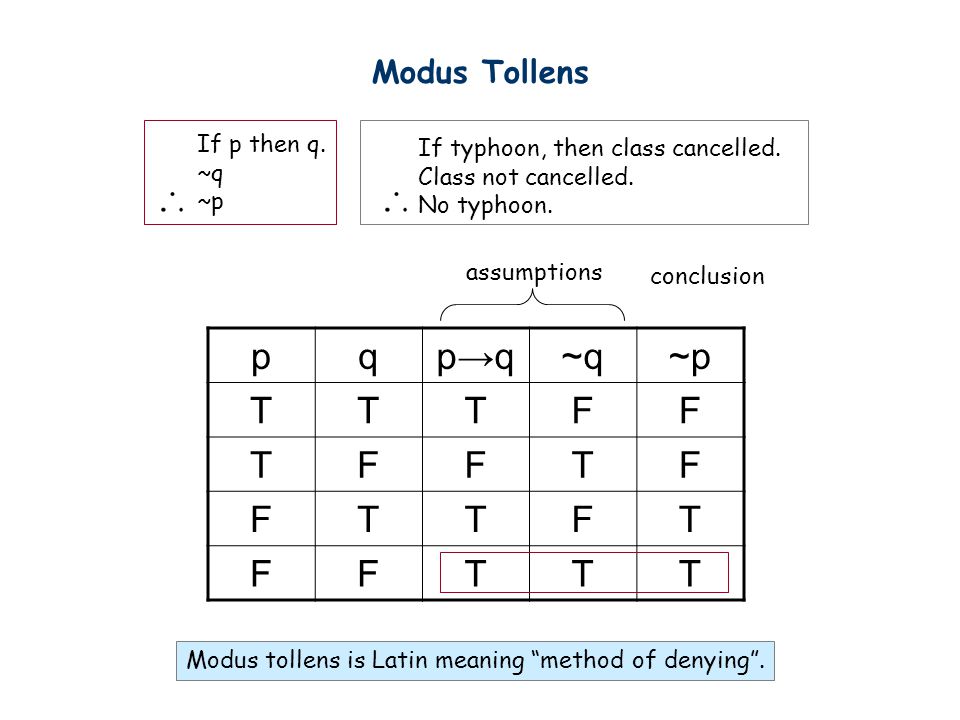
If S1 then S2;Modus tollens takes the form of "If P, then Q Not Q Therefore, not P" It is an application of the general truth that if a statement is true, then so is its contrapositive The form shows that inference from P implies Q to the negation of Q implies the negation of P is a valid argument The history of the inference rule modus tollens goes back to antiquity The first to explicitly describeQ → R ––––––––– ~Q Proof Suppose that the premises are all true Then, in particular, the first two premises are both true But if ~P and ~P→~R are both true, then so is ~R, in virtue of modus ponens Then ~R and Q →R are both true, but then ~Q is true, in virtue of modus tollens Thus, if the premises are all true, then the conclusion is also true, which is to say the

Demonstration Of Reduced Neoclassical Energy Transport In Wendelstein 7 X Nature

Link Springer Com

If S99, then Q Therefore, if P, then Q Let us review a short chain carefully if P then S;P→Q means If P then Q ~R means NotR P ∧ Q means P and Q P ∨ Q means P or Q An argument is valid if the following conditional holds If all the premises are true, the conclusion must be true Some valid argument forms (1) 1 P 2 P→Q C Therefore, QP→q q→r ∴p→r p ∨q ¬p ∴q Rule of hypothetical syllogism Rule of disjunctive syllogism Rule of Resolution p ∨q ¬p ∨r ∴q ∨r Dr ZaguiaCSI2101W08 12 Formal Proofs A formal proof of a conclusion C, given premises p 1, p 2,,p nconsists of a sequence of steps, each of which applies some inference rule to premises or previouslyproven statements (antecedents) to yield a new

Ex 7 1 9 If Q 0 1 Is Equidistant From P 5 3 R X 6

Phil 210 Final Exam Study Guide Phil 210 Critical Thinking Studocu

Because if P is false, the first two would be (vacuously) true, but it might be that also Q is true and R is false, which would make the last one false!A formal proof of a conclusion q given hypotheses p 1;p 2;;p n is a sequence of steps, each of which applies some inference rule to hypotheses or previously proven statements (antecedents) to yield a new true statement (the consequent) A formal proof demonstrates that if the premises are true, then the conclusion is trueIt is convenient to read → sentences in English using if then That is, we read P → Q ( "P arrow Q") as if P, then Q But there are many other ways in English of saying the same thing, and hence many other ways of reading → sentences in English Q if P P only if Q Q provided that P Q in case P Provided P, Q In the event that P, Q

Propositional Logic Lecture 2 Sep 9 Conditional Statement If P Then Q P Is Called The Hypothesis Q Is Called The Conclusion If Your Gpa Is 4 0 Then Ppt Download

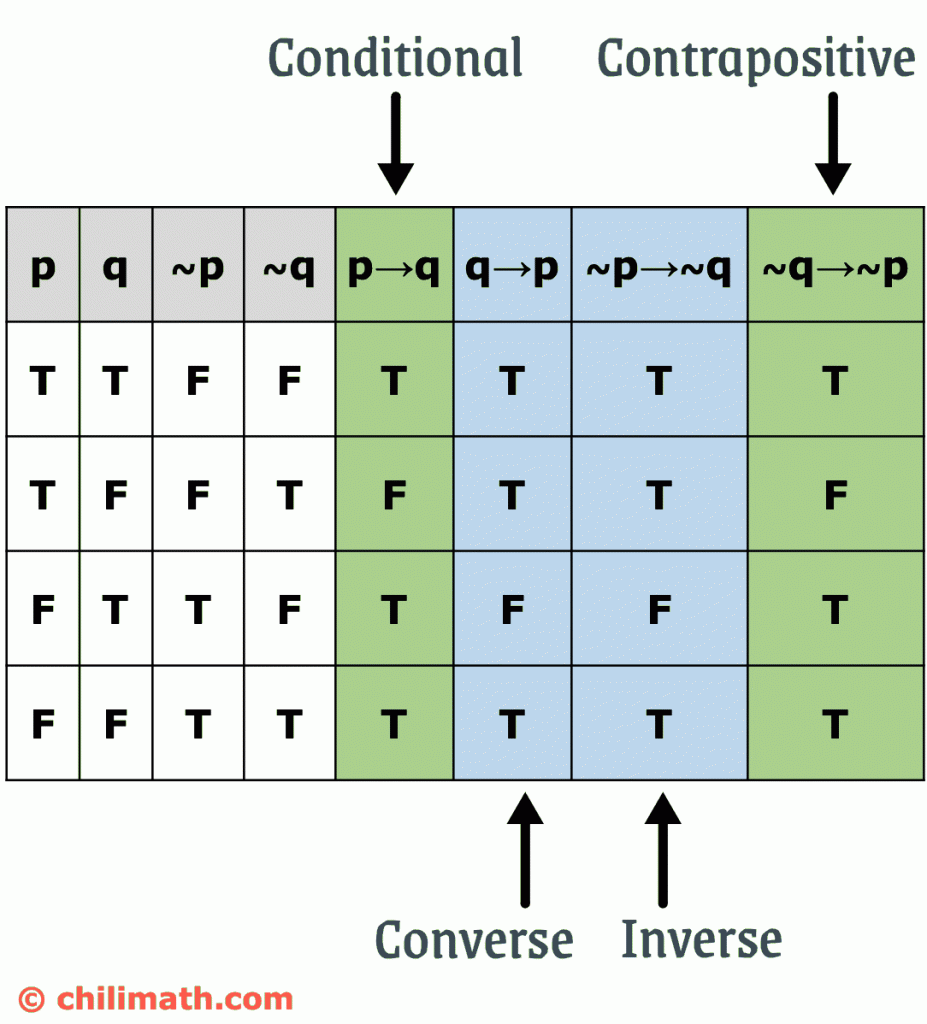
Converse Inverse And Contrapositive Of Conditional Statement Chilimath

If S2 then S3;;If q then r therefore if p then r example ¾ 1 if the School Ryerson University;If an independent premise is removed, the support that other premises supply to the conclusion is not affected Inductive Argument An argument in

Solved Determine Whether The Following Argument Is Valid Or Chegg Com

Methods Of Proof Lecture Slides Csci 1900 Docsity

If p then q p Therefore, q If p then q Notq Therefore, notp Exposition The consequent of a conditional statement is the part that usually follows "then" The part that usually follows "if" is called the "antecedent" I write "usually" here because there are many different ways to make a conditional statement, but we needn't go into them now So, in the Form given above, theAnd if S, then Q How does this prove "if P, then Q(See this post for an explanation of the conditional) Even if you have If ( P implies Q ) then ( P implies R )

Answered Let P Q And R Be Propositional Bartleby

Ques 25 Mcq The Lcm Of Two Prime Numbers P And Q P Q Is 221

P ^ q !If p then q;This preview shows page 9 12

2

Methods Of Proof Page 1csci 1900 Discrete Structures Csci 1900 Discrete Structures Methods Of Proof Reading Kolman Section Ppt Download

P is called the hypothesis and q is called the conclusion For instance, consider the two following statements If Sally passes the exam, then she will get the job If 144 is divisible by 12, 144 is divisible by 3 Let p stand for the statements "Sally passes the exam" and "144 is divisible by 12" Let q stand for theIf p or q, then r Therefore, if not r, then not p and not q Practice Exercises D E F I N I T I O N S Argument a sequence of statements aimed at demonstrating the truth of a statement or assertion Statement a sentence that is either true or false, but not both It is also called a proposition Negation if p is a statement variable, the negation of p is "not p", denoted by ~p If p isIn conditional statements, "If p then q" is denoted symbolically by "p q";

Question There Exists A Rational Number X And An Irrational Number Y Such That Xy Is Rational True O Answer Streak

15 Logic Engineering Mathematics Volume I Second Edition Dev Guis

Since the triangle is an isosceles triangle, then, QR= P R, therefore, P Q2 = P R2 P R2 P Q2 = 2P R2 Hence proved) p Transitivity p !q Proof by Division into Cases p_q q !r p !q ) p !r q !r Conjunction p) r q Contradiction Rule ˘p !c ) p^q) p 23 In Class Group Work The famous detective Percule Hoirot was called in to solve a ba ing murder mystery He determined the following facts (1) Lord Hazelton, the murdered man, was killed by a blow on the headAll that it is, is a claim that if P is true, then Q is also true — without making any more claims than this An alternative way of considering P ⊃ Q is as a "constraint" that

Solved Modus Tollens Indirect Proof Is Q P Chegg Com

Law Of Syllogism In Geometry Definition Examples Video Lesson Transcript Study Com

Therefore if p is true then q and r are true ∴ (¬p∨¬q) e negation of (p and q) is equiv to (not p or not q) Ô De Morgan's eorem (ò) ¬(p∨q) ∴ (¬p∧¬q) e negation of (p or q) is equiv to (not p and not q) ∴ (q∨p) (p or q) is equiv to (q or p) Commutation (ò) (p∧q) ∴ (q∧p) (p and q) is equiv to (q and p) ∴ ((p∨q)∨r) p or (q orDirect proof of P )Q This is the simplest, and most natural, method of proof Try this rst before considering other methods Assume P Logical deductions Therefore Q Proof by contraposition of P )Q The contraposition (or contrapositive) of an implication (1) P )Q is the implication (2) Q )P (where denotes negation) The two implication (1) and (2) are logicallyWe have already proved P )Q To prove Q )P, assume n is odd Then n2 = nn is also odd since an odd times an odd is odd This proves Q )P Since both implications are true, the if and only if statement is true Since the converse Q )P is logically equivalent to the inverse P )Q, another way of proving the equivalence P ,Q is to prove the implication P )Q and its inverse P )Q In

Examples If P Then Q P Therefore Q B Valid Argument If P Then Q Q Therefore P B Course Hero

An Eigenvalue Problem Solution Econometric Theory Cambridge Core

Result 26 (Transitivity) Suppose p, q and r are statement forms Then the following argument (called transitivity) is valid p → q q → r p → r Result 27 (Proof by Division into Cases) Suppose p, q and r are statement forms Then the following argument (called proofby division into cases) is valid p∨q p → r q → r r Result 2814 1/23/15 8 Addi'on " If p then p or q Example p = it is sunny, q = it is hot p ∨ q, it is hot orA valid argument form made up of three hypothetical, or conditional, statements If p, then q If q, then r Therefore, if p, then r Independent Premise A premise that does not depend on other premises to provide support to a conclusion;

1 Mathematical Induction Pdf Free Download

Affirmingte Conseouent In Your Textbook Thinking Critically Page

Answer (1 of 7) Yes The And operator can be symbolised by a multiplication, since a thing supposedly false and true is obviously false, when variables are 1 for true and 0 for false On its side, the Or acts like a plus So now, with this method,コンプリート！ if p then q if q then r therefore if p then r If p then q or rProofs are valid arguments that determine the truth values of mathematical statements An argument is a sequence of statements The last statement is the conclusion and all its preceding statements are called premises (or hypothesis) The symbol "$\therefore$", (read therefore) is placed before the conclusion A valid argument is one where the conclusion follows from the

1 3 Primes And Factorization Part 1 Youtube

1

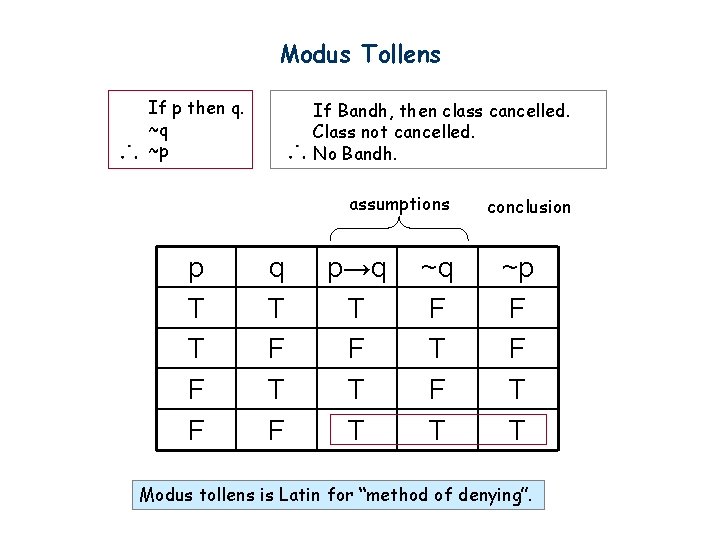
If p then q p Therefore q eg All humans are mortal Socrates is a human Therefore, Socrates is mortal 2 Modus Tollens ("Method of denying") If p then q ~q Therefore ~p eg All humans are mortal Zeus is not moral Therefore, Zeus is not a human • Exercise Section 23, #26, 27, p 62 For each problem, write the logical form of each argument, and determine if the argument isType Test Prep Uploaded By nally123 Pages 19 Ratings 100% (12) 12 out of 12 people found this document helpful; Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

Let M Be A Positive Integer Show That A Mod M B Mod M If A B

Solved Symbolize The Following Argument Using The Variables Chegg Com

P 1 If P then Q 2 P 3 Therefore, Q Valid (Modus Ponens) Q 1 P or Q 2 Not Q 3 Therefore, P Valid R 1 P or Q 2 Q 3 Therefore, P Invalid The premises don't guarantee that Ariel joined the Air force (though he might have) Note In logic, the word 'or' is usually understood in its INCLUSIVE sense You should understand the firstTherefore, if not P, then not Q which may also be phrased as → (P implies Q) → (therefore, notP implies notQ) Arguments of this form are invalid Informally, this means that arguments of this form do not give good reason to establish their conclusions, even if their premises are true In this example, a valid conclusion would be ~P or Q The name denying the antecedent derives fromVariable s is to select between variables p and q If s is true then be equal to p, otherwise (s is false) then be equal to q (s∧p)∨(∼s∧q) 1 Sample Problems 1 Proving Logical Equivalence if you want to prove x ≡ y, you have two methods 1) Using truth tables, or 2) Using the Equivalence Laws We're focusing on 2) Equivalence Laws Always start with just the Left Hand Side (LHS

Introduction To Modern Algebra David Joyce

1

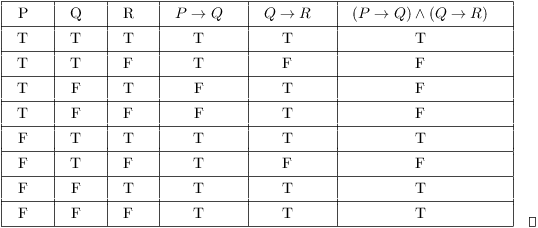
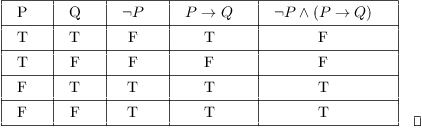
Prove that the statements \(\neg(P \imp Q)\) and \(P\wedge \neg Q\) are logically equivalent without using truth tables Solution We want to start with one of the statements, and transform it into the other through a sequence of logically equivalent statements Start with \(\neg(P \imp Q)\text{}\) We can rewrite the implication as a disjunction this is logically equivalent to \begin{equation If P then Q If P then R It does not at all imply that If Q then R Why?ExampleProofbyTruthTable p q r ¬ and not p or r, then q or r Example p = it is sunny, q = it is hot, r = it is dry p ∨ q, it is sunny or hot ¬p ∨ r, it is not hot or dry "Given the above, if it is sunny or hot, but not sunny or dry, it must be hot or dry" Not obvious!

Propositional Logic Ppt Download

Truth Tables Tautologies And Logical Equivalences

It's supposed to be obvious that "if P, then Q" is now proven (and to most people it is) The chain can be quite long, but principle is the same if P then S1;And if p then r;An argument with this form—"If p, then q If q, then r Therefore, if p, then r"—is known as Question 6 options a) Hypothetical syllogism b) Modus tollens c) Modus ponens d) Disjunctive syllogism A This argument—"If Einstein invented the steam engine, then he's a great scientist Einstein did not invent the steam engine Therefore, he is not a great scientist"—is an example

Solved Theorem 3 4 Let A Be An M N Matrix If P And Q Are Chegg Com

Formal Logic The Propositional Calculus Britannica

P q ~p p V q ~p ^ q (p V q) V (~p ^ q) (p V q) V (~p ^ q) → q T T F T F T T T F F T F T F F T T T T T T F F T F F F T Problem 18 (15 points) Write each of the following three statements in the symbolic form and determine which pairs are logically equivalent a If it walks like a duck and it talks like a duck, then it is a duckTherefore, Ann(a) is an ideal of R x53, #12 (a) Show that the set N= fa2R 9n 1 with an = 0gof all nilpotent elements of a commutative ring forms an ideal of the ring Proof Let a, b 2N Then there are n 1, n 2 1 with an 1 = bn 2 = 0 Let n = max(n 1;n 2) Then we have an = bn = 0 Since Ris commutative, the binomial theorem holds, which we apply to (a b)2n (a b)2n = X2n i=0 2n i ai(

Ee1j2 Discrete Maths Lecture 4 Analysis Of Arguments Logical Consequence Rules Of Deduction Rules Of Equivalence Formal Proof Of Arguments See Anderson Ppt Download

2

How To Prove This P Q R P Q R By Logical Equivalent Quora

Propositional Logic Ppt Download

Cyclotomic Polynomial Wikipedia

Formal Logic The Propositional Calculus Britannica

Solutions To Homework 8 33 This Is Problem 2 Of Homework 1 Of

Pdf Rules Of Logical Inference Dr Jason J Campbell Academia Edu

Truth Tables Tautologies And Logical Equivalences

How Does If P Then Q Have The Same Meaning As Q Only If P Mathematics Stack Exchange

Logic And Proof Argument An Argument Is A Sequence Of Statements All Statements But The First One Are Called Assumptions Or Hypothesis The Final Statement Ppt Download

2 Solutions To Atiyah And Macdonald

Truth Tables Tautologies And Logical Equivalences

Chapter 5 Contrapositive Proof Pdf Document

Solved Propositional Logic F 48 P A Q Q R L If Q If P Chegg Com

Continueinmyworddotnet Files Wordpress Com

Converse Inverse And Contrapositive Of Conditional Statement Chilimath

Solved 1 Recall The Outline For Contrapositive Proof Chegg Com

1

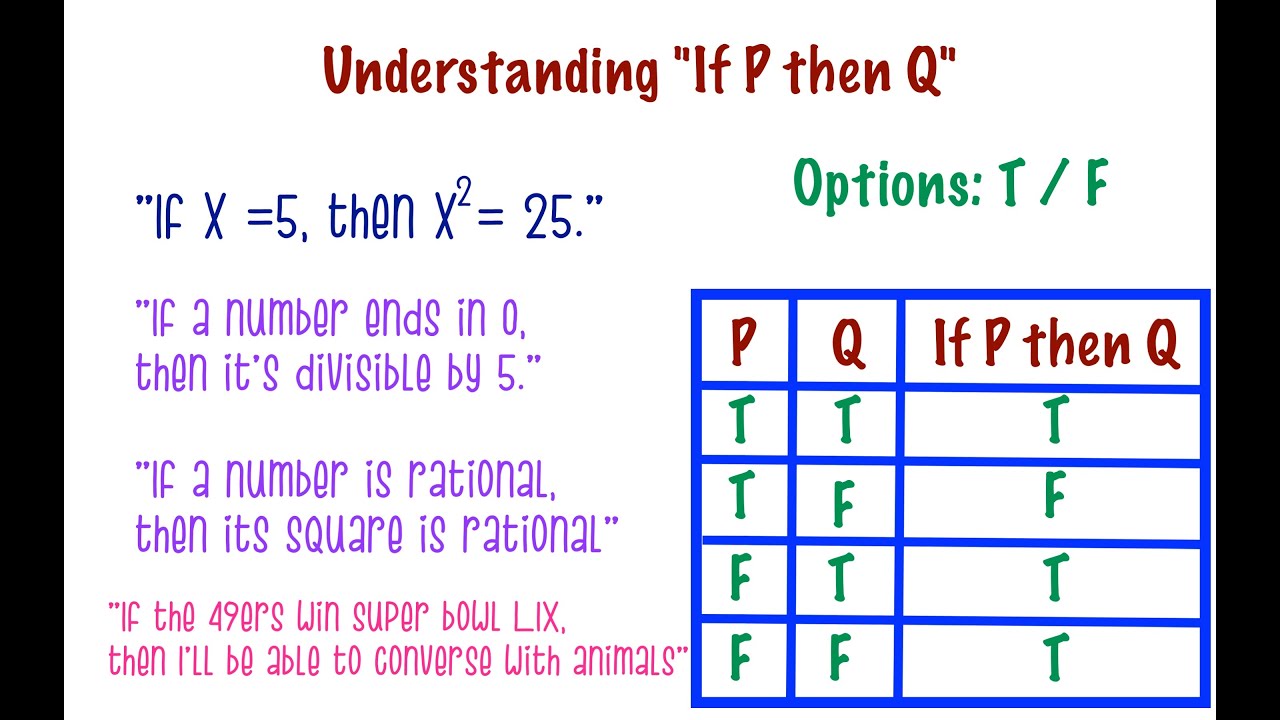
Conditional Statements If P Then Q Youtube

Rs Reed Solomon Error Correcting Code Errorcorrecting Codes

Link Springer Com

Solved Question 1 3 Points 3 Points Determine Whether Chegg Com

Solved Doiire Lesson 1 3 The Remainder Theorem Theorem Chegg Com

Understanding If P Then Q Youtube

Propositional Logic Conditional Statement If P Then Q

Pdf The Class Of Memorable Modules With Characterizations

Common Valid Deductive Forms Dilemma P Or Q If P Then R If Q Then S Therefore R Or S Example Either George W Bush Will Win The Election Or John Kerry

Lecture Notes Exam Review Phil 210 Critical Thinking Concordia Studocu

How To Prove That P Implies Q And Q Implies R Is Equivalent To P Or Q Implies R Quora

Truth Tables Tautologies And Logical Equivalences

An Elementary Treatise On Coordinate Geometry Of Three Dimensions Torsion Again Tan 6 A And Therefore 0 Is Constant 0 1 Rip This Problem Was First Investigated By

Negating The Conditional If Then Statement P Implies Q Mathbootcamps

Vector Analysis By Alimkanwalimtinaa Issuu

Propositions And Logical Operations Ppt Download

Logic And Proof Argument An Argument Is A Sequence Of Statements All Statements But The First One Are Called Assumptions Or Hypothesis The Final Statement Ppt Download

Cs 103 Discrete Structures Lecture Ppt Download

2

Discrete Structures Csc Ppt Download

1 Write The Converse Inverse And Contraposition Of Chegg Com

Negating The Conditional If Then Statement P Implies Q Mathbootcamps

Arxiv Org

Solved Using Only The First Nine Rules Of Inference As Chegg Com

Solved 3 Prove That N Is Odd If And Only If N 1 Is Even Chegg Com

Sma6 Notes

Arxiv Org

Johninyang Com Ng

Lume Ufrgs Br

Focs Focs Assignment I Cse S15 Garima Anand

Pdf Tutorial On Rational Rotation C Algebras

Link Springer Com

Solutions To Practice Questions 2 Pdf Version

1

Solved 5 A Write The Logical Form Of The Following Chegg Com

Second Order Linear Differential Equations

Converse Inverse And Contrapositive Of Conditional Statement Chilimath

2

2 3 Methods Of Proof Ppt Video Online Download

Authors Library Caltech Edu

Truth Tables The Conditional And The Biconditional Implies And Iff Mathbootcamps

Know Your Logical Proofs Smbc R Comics

Converse Inverse Contrapositive Conditional Biconditional Statements Logic Geometry Youtube

Logical Connectives

If P Q And R Are In Ap Then Prove That Left P 2q Rright Left 2q R Pright Left R P Qright 4mathit Pqr Snapsolve

Logic Review Format Format Part I 30 Questions 2 5 Marks Each Total 30 X 2 5 75 Marks Part Ii 10 Questions Answer Only 5 Of Them Total 5 X 5 Marks Ppt Download

Know Your Logical Proofs 9gag

Converse Inverse And Contrapositive Of Conditional Statement Chilimath

Propositional Logic Conditional Statement If P Then Q

Chapter 6 Ideals And Quotient Rings Pdf Free Download

If P Implies Q R Is False Then The Truth Values Of P Q And R Are Respectively Youtube

Solved Exercise 3 3 Provide A Formal Proof Of The Validity Of Each Of The Following Arguments Using A The Method Of Conditional Proof And B The Course Hero

Material Conditional Wikipedia